2022-12-08

良い加減、目覚めましょう

被害者の声
①YouToube削除動画【切り抜き】令和4年11月25日「新型コロナワクチン接種と死亡事例の因果関係を考える」勉強会

 被害統計
②YouToube削除動画【切り抜き】令和4年11月25日「新型コロナワクチン接種と死亡事例の因果関係を考える」勉強会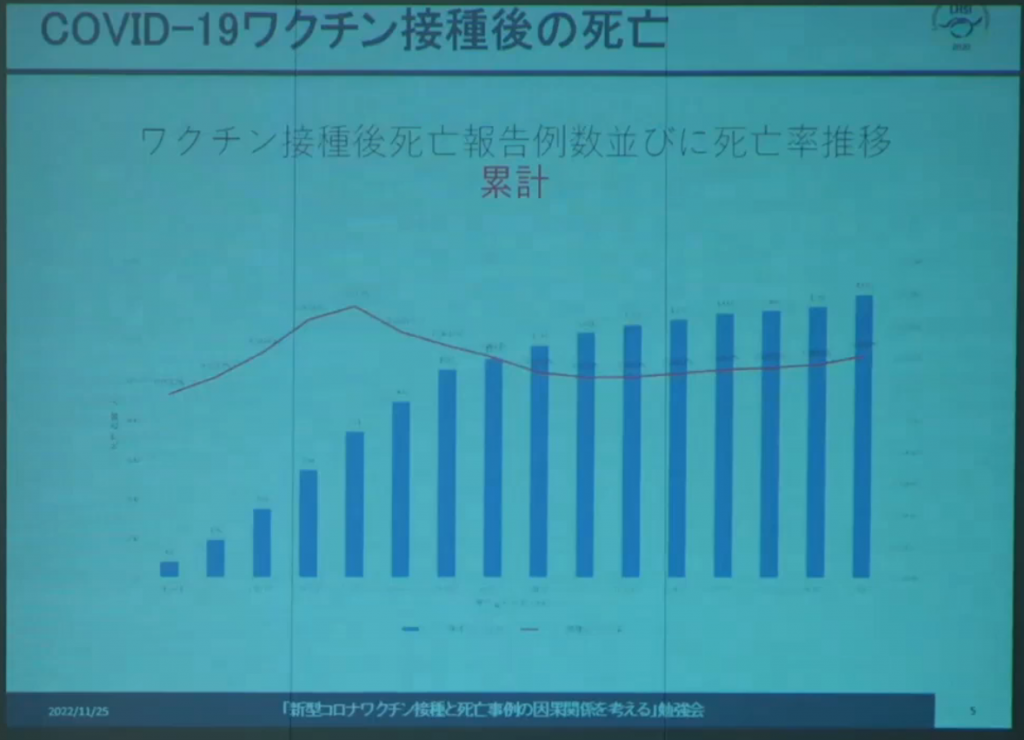

 高知大学　佐野特任教授
③YouToube削除動画【切り抜き】令和4年11月25日「新型コロナワクチン接種と死亡事例の因果関係を考える」勉強会

 名古屋大学　小島勢二名誉教授
④YouToube削除動画【切り抜き】令和4年11月25日「新型コロナワクチン接種と死亡事例の因果関係を考える」勉強会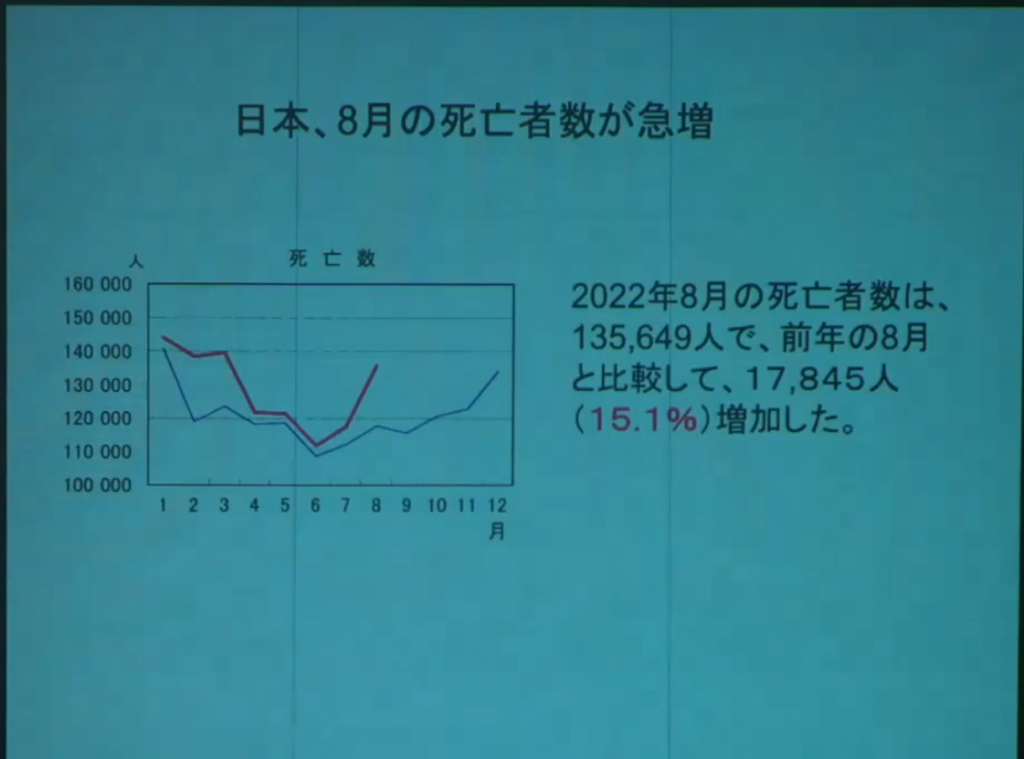
超過死亡数

 ⑤YouToube削除動画【切り抜き】令和4年11月25日「新型コロナワクチン接種と死亡事例の因果関係を考える」勉強会

 【福島節全開】－新型コロナワクチン接種と死亡事例の因果関係を考える勉強会

2022-03-03

Proof of Collatz conjecture

Convergence of $\boldsymbol{log_2 3\hspace{2pt}/\hspace{2pt}2}$

From Wikipedia "Collatz Conjecture"

The Collatz conjecture in mathematics asks whether repeating two simple arithmetic operations will eventually transform every positive integer into one. It concerns sequences of integers in which each term is obtained from the previous term as follows: if the previous term is even, the next term is one half of the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1. The conjecture is that these sequences always reach 1, no matter which positive integer is chosen to start the sequence.

Consider the following operation on an arbitrary positive integer:

If the number is even, divide it by two.
If the number is odd, triple it and add one.

We show two methods, which are said to be the conditions for confirming the end state of the Collatz problem and proof of it.

Check the end status

1. The value does not circulate

The value does not circulate for each individual operation
No value circulation due to multiple operations

2. The value does not spread

In binary numbers, the growth rate of the lowest digit is sufficiently higher than that of the highest digit
Judgment of the state where the value expands
The expanding state is finite
When repeated occurrences and disappearances, the growth rate of contraction is sufficiently higher than the growth rate of expansion

Check the end status

For the Collatz problem, perform operation 5

At this point, 16 is 2 to the 4th power, so it can be seen that it ends. In binary

Will be. Next, if you dare to perform an operation on 1, which is the convergence value,

Will be. As a result, it can be seen that the value in which several two digits of the binary number 01 are lined up converges to 1. As shown shortly after, there is no other case. Hereafter, unless otherwise specified, the numbers in the formula are binary numbers, the numbers in parentheses are decimal numbers (example "1001(9)"), and the numbers after the comma are the remainder numbers of 3 (example "1011(11,2)").

Example of not converging to 1 with one odd number of operations:

When two 1s are adjacent

When two 1s are two digits apart

Example of converging to 1 with one odd number of operations:

When 10 01s are lined up

If you calculate this in decimal,

There is virtually no point in dividing an even number by 2, and these are "multiples of 2", which is a state in which the most significant digit and the least significant digit of the value of 1 when viewed in binary are one.

In other words, the essence of the Collatz problem is that "when an odd number of operations $\boldsymbol{N \times 3 + 1}$ is repeated, it always becomes a multiplier of 2." However, what is added after multiplying by 3 is not 1 but the same value as the minimum digit of the value of 1 in the binary value.

The calculation result is not congruent with 0 with 3 as the modulo. This is because the odd-numbered operation result $N \times 3 + 1$ is always congruent with 1 with 3 as the modulo, so there is no 3 in the factor of that number.

[Reason why values do not circulate]

The value does not circulate for each individual operation

If the values circulate, which of the three operations listed below is performed?

First, assuming that it circulates in $N \times 3$ , if the value to be calculated at the beginning is $N_1$ , the value after the calculation is $M_1$ , the value to be circulated is $N_2$ , and the circulated value after the calculation is $M_2$ ,


 (a)
 (b)

Substituting (a) into (b)

It is inconsistent with $\boldsymbol{N_1 \neq N_2}$ . This assumes that there is a value before the operation, but what about the initial value without the value before the operation?

However, the initial value without a value before the calculation is a multiple of 3, and since the multiple of 3 does not appear after the calculation, it will not be the same value. It is clear that $\boldsymbol{N + 1}$ also gives him the same contradictory results as $\boldsymbol{N \times 3}$ .

$\boldsymbol{N / 2^{n}}$ is also inconsistent if the indices are equal.

However, $N / 2^{n}$ may be equal after the operation due to the difference in the exponents. In fact, if it becomes 29 or 117 after performing several operations from 7 as shown below, the same value will be obtained in even-numbered operations, but is it possible that it is an actual continuous operation?

The fact that the order of the upper digits 0 and 1 is the same and only the number of the lower 0s is different after the odd number operation does not appear in the operation starting from a multiple of the initial value 3 to becoming 1. It corresponds to the confluence when the initial value, a multiple of 3, is started with another value. Therefore, even the operation of $\boldsymbol{N \times 2^{n}}$ does not circulate.

No value circulation due to multiple operations

The fact that the values circulate means that those values do not appear until the operation is repeated and converged to 1.

Assuming that there is a 1 in the upper digit, if you perform operations on the lowest digit continuously as shown below, you can see that all the digits are valid without being missed(The even operation $N / 2^{n}$ is omitted to fix the digit, and +1 in the odd operation conversely performs $+ 1 \times 2^{n}$ ).

If some digits are not valid, they may not converge to 1. It happens by removing the least significant digit in the case of his $N\times3-1$ , which is a variant of odd operations.

Looking at the number that converges to 1 by this operation, the minimum value is 3 and the second place is 11, and 5, 7 and 9 in between do not converge to 1 and circulate, but this is due to -1. This is because the lowest value is not valid. 5 and 7 go directly, 9 goes to 13, 19, and 7 and circulates.

[Reason why the value does not spread]

The diffusion of values occurs when the calculation result expands on average. Individual expansion is due to odd number of operations.

In binary numbers, the growth rate of the lowest digit is sufficiently higher than that of the highest digit.

The final convergence to 1 means that the least significant digit 1 in the binary number catches up with the most significant digit 1 when only odd-numbered operations are performed(Here, the blue 1 becomes the red 1).

Normal      Odd-only             Opening
 operations  operations           of top and bottom digits

Since the most significant digit in binary is tripled, $log_2 3 = 1.58$ digits in a stable state. The last 0, which is the extension of the lowest digit, is definitely one digit by +1. If the adjacent high digit is 0, it becomes 2 by the carry.

 Double digit growth
 Single digit growth

The probability of being vacant from the adjacent high-order digit to the end is

Therefore, the extension is two digits as in the case where the adjacent high-order digits are 0. Therefore, the ratio of growth between the most significant digit and the least significant digit is $1.58 / 2 = 0.79$ . This is a sufficient ratio to converge, and if it is not an infinite value, it will eventually converge to 1.

７Trends in growth of the most significant digit and the least significant digit using 7 as an example

Number of operations	Normal operation		Odd-only operations		Number of digit growth
Number of operations	Normal operation		Odd-only operations		Most significant digit	Last digit
0	111	7	111	7	0	0
1	1011	11	10110	22	2	1
2	10001	17	1000100	68	4	2
3	1101	13	11010000	208	5	4
4	101	5	1010000000	640	7	7
5	1	1	100000000000	2048	9	11

Growth rate of the highest digit (1.8) = Number of growth of digits (9) / Number of operations (5)
Growth rate of the lowest digit (2.2) = Number of growth of digits (11) / Number of operations (5)
Growth rate ratio (0.818) = Growth rate of the highest digit (1.8) / Growth rate of the lowest digit (2.2)

Growth rate ratio between upper digit and least significant digit (value only is binary)

Kinds	Value / Number of digits	Number of operations	Most significant digit		Last digit		Growth rate ratio (Most digit / Least significant digit)
Kinds	Value / Number of digits	Number of operations	Number of digits	Growth rate	Number of digits	Growth rate	Growth rate ratio (Most digit / Least significant digit)
0	11(3)	2	4	2	5	2.5	0.8
0	101(5)	1	2	2	5	5	0.4
0	111(7)	5	9	1.8	11	2.2	0.818
0	1001(9)	6	10	1.667	13	2.167	0.769
0	1011(11)	4	7	1.75	10	2.5	0.7
1	101	528	838	1.587	938	1.777	0.893
2	101	210	334	1.590	434	2.067	0.769
3	101	268	427	1.593	527	1.966	0.810
1	1001	4923	7805	1.585	8805	1.789	0.886
2	1001	2417	3832	1.585	4832	1.999	0.793
3	1001	2621	4156	1.586	5156	1.967	0.806
1	10001	48126	76280	1.585	86280	1.793	0.884
2	10001	24131	38248	1.585	48248	1.999	0.793
3	10001	24300	38546	1.586	48546	1.998	0.794

Kinds

0: Value
1: 111...111
2: 100...001
3: 11

Judgment of the state where the value expands

The operation result of $\boldsymbol{(N \times 3 + 1) / 2}$ becomes an odd number is the maximum value of the number congruent with 2 modulo 3, and only in this case, it is expanded even if an even number operation is performed. This is limited to the case where the least significant two digits of the value before the operation are 11, for the following reasons.

Three times the number 100, which is one larger than 11, is congruent with 0 with 3 as the modulo ... (a)
Multiplying 11 and adding 1 makes it congruent with 1 with 3 as the modulo ................... (b)
If you add both, you can divide by 2, and if you divide by 2, you get an odd number ....... (c)
The above calculation result is congruent with 2 with 3 as the modulo ............................. (d)

(a)
(b)
(c)
(d)

Since 3 times the binary number 100 is congruent with 0 modulo 3, 3 times the binary number whose last 2 digits are 00 is always congruent with 0 modulo 3.
Therefore, if the last two digits are 11, all odd numbers are calculated to be the maximum value of a number congruent with 2 modulo 3.

The expanding state is finite

When multiplying by 3 with consecutive 1s in the upper digit, the last 2 digits are always 01, the first 2 digits are 10, and the middle is filled with 1. This is because there is no carry from the bottom and the top 1 is cut off.

If there is a continuous 1 in the lowest digit, adding 1 makes the continuous 1 a value one digit less than before the operation. That is, when the calculation is repeated in these states, the value expands by the number of consecutive one digit and then converges.

Therefore, the expansion depends on the continuous 1s of the lowest digit in the value before the operation, but if the number of consecutive 1s is finite, it will eventually converge.

Example of expanding and then reducing for two consecutive times:

When repeated occurrences and disappearances, the growth rate of contraction is sufficiently higher than the growth rate of expansion.

Looking at the one with a small value of the lowest digit 11 that can be expanded

This cannot occur because 11 (3,0) is a multiple of 3.
111 (7,1) is caused by 1001 (9,0).

Since 9 is also a multiple of 3, this cannot be generated, but this can be avoided by adding the binary number 10 to the adjacent high-order digits, and the number of 11 to be generated can be increased by the same number of digits.

Condition to expand the generated value (There are 3 or more consecutive 1s in the lowest digit, and the number increases by 2 digits)

Condition to generate an expanded value (the least significant digit is 01 and one or more 10s in the adjacent high digit)

The condition for generating an expanding value and the condition for arranging 01 for reducing digits are values in which the order of 0 and 1 after the third digit is reversed, and it can be said that the probabilities of generating these are equal. However, the number of enlargement / reduction operations is different, and enlargement (number of enlargement digits) > reduction (1).

    Reduction


    Expansion

As for the growth rate between the most significant digit and the least significant digit, if the number of digits of the initial value is set to T, the number of expansion operations is $T-2$ ,

    Reduction calculation





    Expansion calculation

The growth rate of the most significant digit at the expanded value is not accurate, but the calculated value as $log_2 x(x=3.5)$ is $8.81$ , but it is less than 8 in the actual calculation. Therefore, if the elongation of the highest digit is 8, the ratio to the reduced value is 1: 4, and even if the expanded value is generated and expanded repeatedly, it will finally converge. Furthermore, for reduction with a small number of operations, reduction with $log_2 3 / 2$ as a ratio is added by the difference in the number of operations (enlargement (T-1) -reduction (1) = (T-2)).

When the operation is performed with the number of digits T = 114, the following results are obtained. In the case of reduction, only one operation is always performed, so the difference increases as the number of digits increases.



State to shrink
Initial value (114 digits)
010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101
Operation result-End of reduction
1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Number of operations 1 time

State that keeps expanding
Initial value (114 digits)
101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101001
Calculation result-End of expansion (number of digits 293, least significant digit 179)
10110111000000110100000101010111100111010000101001010001011101110100101110111110111001100111100010000110000011010010010101101100001000010001100011100111000110100110110010110000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Number of operations 113 times

In addition, although the value to be expanded can be obtained in other states such as $11101(29,2)$ , the density of 1 becomes high ( $density \gt 1/2$ ), which causes unnecessary values and digits to be expanded. Efficiency (number of enlargements / number of digits of initial value) becomes worse.

From the above

Even if the operation $(N \times 3 + 1) / 2^{n}$ is repeated, it does not circulate and does not spread.
∴ Collatz's prediction is correct

Written notice.
I translated from Japanese original in machine translation software on the Internet. I translated it into Japanese with the same software and confirmed it, but I think there are imprecise and unclear places.

The original text is below.
コラッツ予想の証明 - $log_2 3\hspace{2pt}/\hspace{2pt}2$ の収束

2022-02-11

コラッツ予想の証明

$\hspace{20pt}\boldsymbol{log_2 3\hspace{2pt}/\hspace{2pt}2}$ の収束

ウィキペディア「コラッツの問題」より

任意の正の整数 n に対して、以下で定められる操作について考える。

n が偶数の場合、n を 2 で割る
n が奇数の場合、n に 3 をかけて 1 を足す

このとき、「どんな初期値から始めても、有限回の操作のうちに必ず 1 に到達する（そして 1→4→2→1 というループに入る）」という主張が、コラッツの予想である。

コラッツの問題における終了状態の確認と、その証明の条件と言われている２点の方法を示す。

終了状態の確認

１．値が循環しないこと

個別の演算ごとに値が循環しないこと
複数の演算による値の循環がないこと

２．値が拡散しないこと

２進数値において、最上位よりも最下位桁の伸び率の方が十分に高いこと
値が拡大する状態の判定
拡大する状態が有限であること
発生、消滅を繰り返す場合、拡大の伸び率よりも縮小の伸び率の方が十分に高いこと

終了状態の確認

コラッツの問題について、５の演算を行なう。

この時点で、１６は２の４乗なので終了するのが分かる。２進数にすると

となる。次に収束値である１について、あえて演算を行なうと

となる。これによって、２進数の０１の２桁がいくつか並んだ値が１に収束する状態であると分かる。すぐ後に示すように、それ以外の場合はない。以後、特に断りのない限り数式内の数値は２進数とし、括弧内を１０進数（例「1001(9)」）、カンマの後の数字は３の剰余数（例「1011(11,2)」）とする。

奇数の演算１回で１に収束しない例：

２つの１が隣接している場合

２つの１が２桁離れている場合

奇数の演算１回で１に収束する例：

０１を１０個並べた場合

これを１０進数で演算すると

これらは偶数を２で割ることに実質的な意味はなく、２進数で見た時の１の値の最上位桁と最下位桁が一つになった状態「２の乗数」になるということである。

つまり「奇数の演算 $\boldsymbol{N \times 3 + 1}$ を繰り返すと必ず２の乗数になる」というのがコラッツの問題の本質である。ただし３を掛けた後に加えるのは１ではなく、２進数値での１の値の最小位桁と同じ値であること。

演算結果が３を法として０と合同になることはない。これは奇数の演算結果 $N \times 3 + 1$ では必ず３を法として１と合同となるのだから、その数の因数に３が無いことによる。

【値が循環しない理由】

個別の演算ごとに値が循環しないこと

仮に値が循環するとして、それは以下に挙げた３種類ある演算のどれを行った時か。

まず $N \times 3$ で循環するとして、初めの演算をする値を $N_1$ 、その演算後の値を $M_1$ 、循環する値を $N_2$ 、その演算後の循環した値を $M_2$ とすれば


 (a)
 (b)

(a)を(b)に代入すると

となり $\boldsymbol{N_1 \neq N_2}$ と矛盾する。これは演算前の値があることを想定したのだが、演算前の値のない初期値ではどうか。

だが演算前の値がない初期値というのは３の倍数であり、演算後に３の倍数は現れないのだから同じ値になることもない。 $\boldsymbol{N + 1}$ も $\boldsymbol{N \times 3}$ と同様に矛盾する結果になるのは明らか。

$\boldsymbol{N / 2^{n}}$ も指数が等しければ矛盾となる。

しかし $N / 2^{n}$ は指数に差が出ることにより演算後に等しくなる可能性がある。事実、以下のように７から数回の演算を行った後に２９あるいは１１７となった場合、偶数の演算で同じ値となってしまうが、実際の連続する演算ではあり得るか。

このように奇数の演算後に上位桁の０と１の並びが等しく下位０の数だけが異なるというのは、初期値３の倍数から始めて１になるまでの演算の中に現れることはなく、それは初期値である３の倍数を別の値で始めた場合の合流点に当る。したがって $\boldsymbol{N \times 2^{n}}$ の演算でも循環することはない。

複数の演算による値の循環がないこと

値が循環するということは、演算を繰り返して１に収束されるまでに、それらの値が現れないということである。

上位桁に１があるとして、以下のように最下位桁に連続で演算を施すと、取りこぼしなく、すべての桁が有効であるのが分かる（桁を固定するために偶数の演算 $N / 2^{n}$ を省略し、奇数の演算における＋１は逆に $+ 1 \times 2^{n}$ を行なう）。

もし有効ではない桁があれば、それによって１に収束しないものもあり得る。それは奇数の演算を変形した $N\times3-1$ の場合、最下位桁を削除することにより起こる。

この演算で１に収束する数をみていくと最小値が３、第２位が１１であり、その間の５，７，９は１に収束せずに循環してしまうが、これは－１により最下位の値が有効にならないためである。５，７は直接，９は１３，１９，７へと推移して循環する。

【値が拡散しない理由】

値の拡散は演算結果が平均して拡大していくことにより起こる。個々の拡大は奇数の演算による。

２進数値において、最上位よりも最下位桁の伸び率の方が十分に高いこと

最終的に１に収束するというのは、奇数の演算だけを行った場合、２進数での最下位桁の１が最上位桁の１に追い付くということである（ここでは青の１が赤の１に）。

通常の演算　　　奇数だけの演算　　　最上位と最下位桁の開き

２進数での最上位桁は３倍になるのだから安定した状態では $log_2 3 = 1.58$ 桁の伸びである。最下位桁の伸びである末尾の０は＋１により確実に１桁はあり、隣接する上位桁が０であれば桁上げにより２となる。

　　２桁の伸び
　　１桁の伸び

隣接する上位桁から先の先まで空いた場合の確率は

であり、隣接する上位桁が０の場合と同じく２桁の伸びとなる。したがって最上位桁と最下位桁の伸びの比率は $1.58 / 2 = 0.79$ である。これは収束するには十分な比率であり、無限の値でなければ最後は１に収束する。

７を例にした最上位桁と最下位桁の伸びの推移

演算回数	通常の演算		奇数だけの演算		桁の伸び数
演算回数	通常の演算		奇数だけの演算		最上位桁	最下位桁
0	111	7	111	7	0	0
1	1011	11	10110	22	2	1
2	10001	17	1000100	68	4	2
3	1101	13	11010000	208	5	4
4	101	5	1010000000	640	7	7
5	1	1	100000000000	2048	9	11

最上位桁の伸び率(1.8)＝桁の伸び数(9) ／演算回数(5)
最下位桁の伸び率(2.2)＝桁の伸び数(11)／演算回数(5)
伸び率比(0.818)　　　＝最上位桁の伸び率(1.8)／最下位桁の伸び率(2.2)

上位桁と最下位桁の伸び率比（値のみ２進数）

種別	値／桁数	演算回数	最上位桁		最下位桁		伸び率比（最上位桁/最下位桁）
種別	値／桁数	演算回数	桁数	伸び率	桁数	伸び率	伸び率比（最上位桁/最下位桁）
0	11(3)	2	4	2	5	2.5	0.8
0	101(5)	1	2	2	5	5	0.4
0	111(7)	5	9	1.8	11	2.2	0.818
0	1001(9)	6	10	1.667	13	2.167	0.769
0	1011(11)	4	7	1.75	10	2.5	0.7
1	101	528	838	1.587	938	1.777	0.893
2	101	210	334	1.590	434	2.067	0.769
3	101	268	427	1.593	527	1.966	0.810
1	1001	4923	7805	1.585	8805	1.789	0.886
2	1001	2417	3832	1.585	4832	1.999	0.793
3	1001	2621	4156	1.586	5156	1.967	0.806
1	10001	48126	76280	1.585	86280	1.793	0.884
2	10001	24131	38248	1.585	48248	1.999	0.793
3	10001	24300	38546	1.586	48546	1.998	0.794

種別

0: 値
1: 111...111
2: 100...001
3: 1<乱数>1

値が拡大する状態の判定

$\boldsymbol{(N \times 3 + 1) / 2}$ の演算結果が奇数になるのは３を法として２と合同な数の最大値であり、この場合のみ偶数演算を施しても拡大する。これは演算前の値の最下位２桁が１１の場合に限るが、それは以下の理由による。

１１より１大きい数100の３倍は３を法として０と合同となる …………(a)
１１を３倍して１を加えると３を法として１と合同となる………………(b)
両者を加えると２で割ることができ、かつ２で割ると奇数になる………(c)
以上の演算結果は３を法として２と合同となる……………………………(d)

(a)
(b)
(c)
(d)

２進数100の３倍が３を法として０と合同となるのだから、下２桁が００の２進数の３倍は必ず３を法として０と合同となる。
したがって、すべての奇数は下２桁が１１であれば演算により３を法として２と合同な数の最大値となる。

拡大する状態が有限であること

上位桁に連続する１がある状態で３倍する場合、下２桁は常に０１、上２桁が１０となり中間は１で詰まる。これは下位からの桁上げがないことと上位の１が途絶えることによる。

最下位桁に連続する１がある場合は１を加える事により、連続する１は演算前より１桁少ない値となる。つまりこれらの状態で演算を繰り返すと、連続する１の桁数分だけ値が拡大し、その後収束することになる。

したがって、拡大は演算前の値における最下位桁の連続する１によるが、連続する１が有限個であればいずれ収束する。

２連続で拡大した後に縮小する例：

発生、消滅を繰り返す場合、拡大の伸び率よりも縮小の伸び率の方が十分に高いこと

拡大できる状態である最下位桁１１の値の小さいものを見ると

11(3,0) は３の倍数であるからこれを発生できない。
111(7,1)は1001(9,0)により発生する。

９も３の倍数であるからこれを発生できないが、隣接する上位桁に２進数１０を追加することによりこれを回避でき、かつ発生させる１１の数を同じ桁数だけ増やすことができる。

発生する値を拡大する条件（最下位桁の連続する１が３桁以上、２桁ずつ）

拡大する値を発生する条件（最下位桁が01で隣接する上位桁に１つ以上の１０）

拡大する値を発生する条件と、桁を減らす０１の並んだ条件は３桁以降の０と１の順番が逆の値であり、これらを生成する確率は等しいと言える。しかし拡大／縮小の演算ではその回数が異なり、拡大（拡大桁数）＞縮小（１）である。

　縮小


　拡大

それぞれの最上位桁と最下位桁との伸び率は、初期値の桁数をTと置くと拡大の演算回数が $T-2$ となり

　縮小の演算


　
　

　拡大の演算

拡大した値での最上位桁の伸び率は正確ではないが $log_2 x(x=3.5)$ としての計算値は $8.81$ であるが実際の演算では８未満となる。そこで最上位桁の伸びを８とすると、縮小した値との比は１：４となり、拡大する値の発生、拡大を繰り返しても最終的に収束することになる。さらに演算数の少ない縮小には、演算回数の差である(拡大(T-1)-縮小(1) = (T-2))により $log_2 3 / 2$ を比率とした縮小が加わるのである。

桁数T=114として演算を行なうと、以下の結果が得られる。縮小の方は常に１回の演算を行なうだけなので桁数が増えれば差も広がるのである。

　

縮小する状態
初期値（桁数１１４）
010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101
演算結果－縮小の終了
1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
演算回数１回

拡大し続ける状態
初期値（桁数１１４）
101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101001
演算結果－拡大の終了（桁数２９３、最下位桁１７９）
10110111000000110100000101010111100111010000101001010001011101110100101110111110111001100111100010000110000011010010010101101100001000010001100011100111000110100110110010110000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
演算回数１１３回

なお、 $11101(29,2)$ のような他の状態でも拡大する値は得られるが、１の密度が高くなる( $密度 \gt 1/2$ )ことにより無駄な値や桁が発生してしまい、拡大効率（拡大回数／初期値の桁数）は悪くなる。

以上から

演算 $(N \times 3 + 1) / 2^{n}$ を繰り返しても循環することはなく、拡散することもない
∴コラッツの予想は正しい

rabbit2202のブログ

コラッツ予想の証明とそれにまつわる記事を書きます

良い加減、目覚めましょう

Proof of Collatz conjecture

コラッツ予想の証明